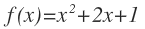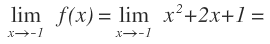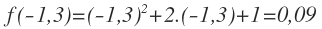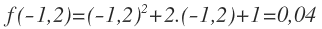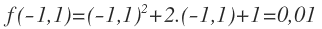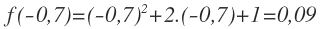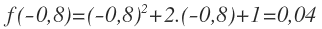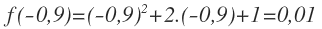EJERCICIO 9
Ejercicio resuelto en clase
Calcular su limite
Comprobar
Resuelto en la aplicación Symbolad
EJERCICIO 10
Ejercicio realizado en clase
Limites
Comprobar
Resuelto en la aplicación calculadora de derivadas
EJERCICIO 11
Ejercicio de derivadas Explicado en clase
Comprobar
Resuelto en la aplicación Symbolad
Resuelto en la aplicación calculadoras de derivadas
EJERCICIO 12
Ejercicio realizado en clase
Comprobar
Resuelto en la aplicación Symbolad
Resuelto en la aplicación calculadoras de derivadas
EJERCICIO 13
Ejercicio resuelto en clase
Comprobar
Resuelto en la aplicación Symbolad
Resuelto en la aplicación calculadoras de derivadas
EJERCICIO 14
Ejercicio resuelto en clase
Comprobar
Resuelto en la aplicación Symbolad
Resuelto en la aplicación calculadoras de derivadas
EJERCICIO 15
Ejercicio resuelto en clase